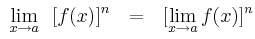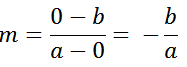La función f es derivable en a si
En este caso el límite se designa por f' (a) y recibe el nombre de derivada de f en a. Decimos también que f es derivable si f es derivable en a para todo a del dominio de f.
martes, 9 de noviembre de 2010
lunes, 8 de noviembre de 2010
Derivadas de funciones
Derivada , notación
Derivadas ordinarias
Se define la derivada de una función como el límite del cociente del cambio en la ordenada y la abscisa. Hay varias notaciones para denotar la derivada de una función de una sola variable:
Las derivadas serian:
La operación fundamental en el cálculo diferencial es encontrar una derivada. Esta tabla enlista las derivadas de varias funciones. En lo sucesivo, f y g son funciones de x y c es una constante con respecto a x. Se presupone al conjunto de los números.
Estas fórmulas son suficientes para diferenciar cualquier función elemental.
domingo, 24 de octubre de 2010
Definición de límite por épsilon-delta
Definición épsilon-delta
Sea f una función definida en algún intervalo abierto que contenga a a.
El límite de f (x) cuando x tiende a es L, y se escribeLa función f(x) tiende hacia el límite L en a cuando, para todo e>0, existe algún d>0 tal que, para todo x que cumple
(Es decir, que lím f(x) = L cuando x->a si y solo si se cumplen las condiciones indicadas.)
Esta definición (E, δ) es el laborioso resultado de más de cien años de intentos teóricos.
Tal definición significa la completa reagudización de un concepto, el de límite, que es indispensable para definir a su vez los dos conceptos fundamentales del cálculo infinitesimal: los de derivada e integral.
lunes, 4 de octubre de 2010
Propiedades de los Límites
Haz clic Propiedades de los límites
1º) Límite de una constante
3º) Límite de la suma algebraica de dos o más funciones
4º) Límite del producto de dos o más funciones
5º) Límite del cociente de dos funciones
6º) Límite de una función elevada a una potencia
7º) Límite de la raíz n-ésima de una función
8º) Límite de una función exponencial
Casos especiales de límite
Para
tenemos que:
Límite de funciones trigonométricas
El límite de una función trigonométrica en un punto dado se obtiene de igual manera que con las funciones algebraicas.
Teorema fundamental de límite
a parti del teorema fundamental tenemos:
viernes, 1 de octubre de 2010
Límite
Idea intuitiva de límite
En esta clase se presenta la idea formal de límite como una operación aplicada a una función en un punto.
Se establecerán también algunos teoremas sobre límites de sumas, productos y cocientes de funciones.
Iniciaremos nuestro estudio con la idea intuitiva de límite.
La presentación de los ejemplos siguientes pretenden dar una idea del significado del límite de una función en un punto.
Consideramos la función definida por
con dominio en los reales R
La representación gráfica es la siguiente:
Nos interesa observar el comportamiento de la función f para los valores de x más cercanos a 2 pero no iguales a 2
Veamos las tablas siguientes
Puede observarse de ambas tablas que conforme se aproxima más a 2, f (x) toma, cada vez, valores más próximos a 3.
Esto puede escribirse utilizando la notación de límites escribimos
que se lee: el límite de f(x) cuando x tiende a 2, es igual a 3
Límite
En matemática, se usa el concepto del límite para describir la tendencia de una sucesión o una función. La idea es que en una sucesión o una función, al hablar de límite, decimos que tiene uno si se puede acercar a un cierto número (o sea, el límite) tanto como queramos.
Límite de una función
Sea f la función definida por la ecuación
para toda
Indeterminaciones
Hay varios tipos de indeterminaciones, entre ellas:
Ejemplo: 0/0 es una indeterminación pues límites de cocientes donde los límites de dividendo y divisor separadamente son cero, pueden terminar dando cualquier cosa, como
para toda
De la gráfica puede observarse que aunque la función f no está definida para x = 2 cuando x toma valores muy cercanos a 2 la función se aproxima a 5, lo que escribimos como:
Indeterminaciones
Hay varios tipos de indeterminaciones, entre ellas:
Ejemplo: 0/0 es una indeterminación pues límites de cocientes donde los límites de dividendo y divisor separadamente son cero, pueden terminar dando cualquier cosa, como
lunes, 27 de septiembre de 2010
Representación Gráfica de las Funciones Trigonométricas

Representación gráfica de una función periódica
En la vida diaria existen muchos casos de funciones periódicas cuando la variable es el tiempo; situaciones como el movimiento de las manecillas de un reloj o las fases de la luna muestran un comportamiento periódico. Un movimiento periódico es aquel en el que la posición(es) del sistema se pueden expresar en base a funciones periódicas, todas con el mismo período.
Para una función aplicada al conjunto de los números reales o al de los enteros, significa que la totalidad de su gráfica puede ser representada a partir de copias de una determinada porción de ésta, repetida a intervalos regulares.
Las funciones trigonométricas seno, coseno típicos de funciones periódicas, cuyo período es 360 grados. En el caso de la tangente, vemos que su periodo es menor, siendo 180 grados.
miércoles, 1 de septiembre de 2010
Ecuación de la Recta.
- Ecuación de la recta.
- Ecuación Principal de la recta.
- Ecuación General de la recta.
- Representación gráfica de la recta.
- Ecuación Simétrica de la recta.
- Teoremas de rectas paralelas.
- Teoremas de rectas perpendiculares.
- Expresión de rectas notables.
La Recta
Se describe como la sucesión continua e indefinida de puntos en una sola dimensión.
Características de la recta
Algunas de las características de la recta son las siguientes:
- La recta se prolonga al infinito en ambos sentidos.
- En la geometría Euclidiana, La distancia más corta entre dos puntos está en una línea recta.
- La recta es un conjunto de puntos situados a lo largo de la intersección de dos planos.
1. Ecuación de la Recta
Cuando se tienen dos puntos cualesquiera
la pendiente queda determinada por el cociente entre la diferencia de las ordenadas de dos puntos de ella y la diferencia de las abscisas de los mismos puntos, o sea
Se puede obtener la ecuación de la recta a partir de la fórmula de la pendiente:
2. La Ecuación Principal de la recta
Si se conoce la pendiente m, y el punto donde la recta corta al eje de ordenadas (0, b), podemos deducir, partiendo de la ecuación general de la recta, y − yo = m(x− xo):
La ecuación principal de la recta, el valor de m corresponde a la pendiente de la recta y b es el coeficiente de posición (corte con el eje y).
3. Ecuacion general de la recta
La ecuación general de la recta es de la siguiente forma
Despejando “y” nos encontramos con la expresión de la ecuación principal :
De donde en la ecuación general:
4. Representación Gráfica de La Ecuación de la Recta
La pendiente m es la tangente de la recta con el eje de las abscisas
Se obtiene la ecuación de la recta con su pendiente y las coordenadas de uno de sus puntos, o cuando se conocen sólo los dos puntos por lo que también se le llama ecuación de la recta conocidos dos puntos.
5. Representación gráfica de La ecuación principal
La ecuación principal se le dice que es la ecuación en forma simplificada.
Esta segunda forma de la ecuación de la recta, se utiliza cuando se conoce la pendiente y la ordenada al origen.
6. Ecuación Simétrica de la recta
Conocidos los puntos con los ejes de coordenada (a,0) y (0,b)
Se calcula la pendiente:
Se sustituye en la ecuación y2 − y1 = m(x2 − x1), usando cualquiera de los dos puntos, en este caso (a, 0):
Se divide toda la ecuación entre el término independiente ab
Se obtiene la ecuación de la recta en su forma simétrica
Esta ecuación se utiliza para obtener la ecuación de una recta conociendo sus intersecciones con los ejes y cuando, a partir de la ecuación de una recta, se desean conocer los puntos donde dicha recta intercepta a los ejes.
Ejercicio 1
Encontrar la ecuación de la recta que pasa por los puntos: (3, -2) y (9, 6)
7. Teorema de Rectas Paralelas
Sean l1 y l2 dos rectas no verticales con pendientes m1 y m2 respectivamente.
Entonces:
Ejercicio 2
Determinar la ecuación de la recta paralela a 3x - 2y + 5 = 0 que pase por el punto A(1,1)
8. Teorema de Rectas Perpendiculares
Sean l1 y l2 dos rectas perpendiculares m1 y m2 respectivamente.
Entonces:
Ejercicio 3
Determinar la ecuación de la recta perpendicular a la del ejercicio2 y que pase por el punto A(2,-3)
9. Rectas notables
Caso 1. Recta paralela al eje x:
Caso 2. Recta paralela al eje y:
Caso 4. Ecuación de una recta que pasa por el origen:
Realizar la actividad del siguiente link
Suscribirse a:
Entradas (Atom)